Варианты

В разделе Списки мы упомянули, что односвязные неизменяемые списки использовались в оригинальной версии Лисп для представления любых данных, будь то структуры данных или программы. Например, выражение a*b + c в Лисп представлено так: (+ (* a b) c). Иначе говоря, на верхнем уровне у нас имеется список из трёх элементов, первым элементом которого является операция +, вторым – вложенное выражение (* a b), третьим – символ c. Такое представление легко выразить в Лисп (или Python), поскольку в этих языках списки гетерогенны. Теперь попробуем воспроизвести подобное в Ficus, используя известные нам типы данных. Быстро выясняется, что попытка терпит неудачу, так как все элементы списка должны принадлежать одному типу, что неверно в приведённом случае. Ещё сложнее оказывается представлять иерархические структуры данных с помощью списков, кортежей, массивов или записей, ведь такие структуры по определению рекурсивны, а изученные нами ранее структуры не поддерживают рекурсию.

Однако существует элегантное и мощное решение проблемы, впервые предложенное языком программирования ML. Называется оно тип-сумма. Почему оно носит название “тип-сумма”? Дело в теории множеств.

Пусть имеются несколько типов: T1, T2, ..., Tn. Каждый тип определяет множество возможных значений, которые могут принимать экземпляры этого типа. Определим теперь кортеж:

type T = (T1, T2, ..., Tn)

Тогда множество значений, которые может принять экземпляр кортежа, будет являться декартовым произведением множеств, определённых типами T1, T2, ..., Tn. Отсюда и принятая в Standard ML и OCaml нотация для кортежей:

(* Определение кортежа в SML/OCaml *)
type T = T1 * T2 * ... * Tn

Но как определить тип, множество значений которого являлось бы объединением, или суммой, множества значений типов T1, T2, ..., Tn? Или, иными словами, мы хотели бы нечто вроде T1 + T2 + ... + Tn. Если удастся определить подобный тип, мы сможем создать разновидность разнородных списков, где каждый элемент может быть одного из типов T1, ..., Tn. Попробуем представить такой “суммарный тип” с помощью записи:

val T1_tag = 1
val T2_tag = 2
...
val Tn_tag = n

type псевдо_суммарный_T =
{
    tag: int
    T1_val: T1
    T2_val: T2
    ...
    Tn_val: Tn
}

Такая конструкция неэффективна по двум причинам:

она крайне расточительна по памяти, так как одновременно используется только одно из полей Ti_val.
конструкция небезопасна, так как можно, полагая, что знаем метку, пропустить проверку и обратиться к какому-то полю Ti_val, хотя реальная метка может отличаться, делая данное поле нерелевантным.

Если бы в Ficus существовал реальный тип-“объединение”, аналогичный типу union в C, это решило бы проблему с памятью, но сделало бы язык опасным. Вместо этого в Ficus предусмотрен безопасный функциональный тип, известный как тип-сумма, алгебраический тип или вариант. Будем чаще употреблять термин вариант.

Вариант определяется следующим образом:

type optional_type_parameters type_name =
    // первая вертикальная черта после знака "=" необязательна
    | Tag1 [: T1]
    | Tag2 [: T2]
    ...

где Tagj – идентификатор, начинающийся с прописной буквы, а Tj – некий тип. Если тип не указан, подразумевается, что он равен void, то есть метка сама по себе полностью определяет соответствующее ей значение и не нуждается в атрибутах. В простейшем варианте вариант может выступать в роли перечисления:

Тип Tj позволяет указать, что вариант содержит вложенные данные и задать их тип.

type month = Jan | Feb | Mar | Apr | May | Jun | Jul
            | Aug | Sep | Oct | Nov | Dec

Однако настоящая сила вариантов раскрывается, когда мы вводим типы для меток. Вот абстрактный синтаксис для подобия Лисп-микроязыка:

type unop = Neg | Head | Tail | Null

type binop = Add | Sub | Mul | Div | Mod | Cons
   | CmpEQ | CmpLT | CmpLE | CmpNE | And | Or

type expr =
   | Num: double
   | Char: char
   | Nil | Void
   | Bool: bool
   | Val: string
   | Binary: (binop, expr, expr)
   | Unary: (unop, expr)
   | Call: (expr, expr list)
   | DefVal: (string, expr)
   | DefFun: (string, string list, expr)
   | If: (expr, expr, expr)
   | Seq: expr list

Заметим, что в некоторых вариантах тип expr рекурсивно ссылается на самого себя. Это значит, что варианты способны представлять рекурсивные структуры данных!

Посмотрим, как определить факториал в этом микроязыке:

val n = Val("n")
val one = Num(1.0)
val f = DefFun("fact", "n" :: [], If(Binary(CmpLE, n, one), one,
            Binary(Mul, n, Call(Val("fact"), Binary(Sub, n, one) :: []))))

Создание экземпляров вариантов в Ficus облегчено благодаря следующему механизму:

метки с параметрами (такие как DefFun) выступают в роли конструкторов, принимающих соответствующие аргументы и возвращающих экземпляр с нужной меткой.
метки без параметров (например, CmpLE) могут использоваться непосредственно как значения. Они также являются конструкторами, просто записанными в виде значений, а не функций (следовательно, используется CmpLE, а не CmpLE()).

Итак, создав экземпляр варианта, мы можем попытаться каким-то образом его обработать. Тогда как для других функциональных типов (кортежи, списки) существуют специальные методы доступа (. для записей, List.hd() и List.tl() для списков), для вариантов доступна единственная возможность – сопоставление с образцом. Давайте реализуем часть интерпретатора нашего мини-Лисп языка:

type entry_type = ValEntry: (string, expr) | FunEntry: (string, expr)

type env_t = entry_type list

fun eval(e: expr, env: env_t): (expr, env_t) =

match e {
  | Binary(bop, e1, e2) =>
  val e1_ = eval(e1, env)
  val e2_ = eval(e2, env)

  // В сопоставлении с образцом нередко используется следующий трюк.
  // Формируется кортеж из нескольких значений,
  // а затем используется как образец кортежа.
  // то есть,
  //    match (expr1, expr2, ..., exprN) {
  //    | ...
  //    | (pat1, pat2, ..., patN) => ...
  //    | ...
  //    }
  // эмулирует что-то вроде следующего:
  //     ... else if expr1 matches pat1 &&
  //              expr2 matches pat2 && ...
  //              exprN matches patN { ... }
  //
  (match (bop, e1_, e2_) {
    | (Sub, Num(n1), Num(n2)) => Num(n1 - n2)
        ...
    | (CmpLE, Num(n1), Num(n2)) => Bool(n1 <= n2)
        ...
    }, env)

  | DefVal(v, e) =>
  val e_ = eval(e, env)
  // Добавляем пару (v, e) в окружение
  (Void, ValEntry(v, e_) :: env)

  | Call(e, args) =>
  // Вычисляем e, args
  // находим функцию в окружении,
  // затем добавляем пары (formal_arg, arg_value) 
  // в окружение и, наконец, вычисляем тело.
    ...
...
}

Варианты и оператор match очень просты в использовании и выглядят как другие образцы. Вы ставите имя метки и другие образцы внутрь скобок (), так, словно конструируете экземпляр варианта. Проверка проводится сначала по метке, а затем сверяются вложенные образцы и захватываются, если нужно, переменные.

Использование вариантов совместно с оператором match решает обе проблемы наивной реализации объединений:

безопасность обеспечивается тем, что сравнение метки и выбор нужных данных происходят одновременно, исключая возможность доступа к неправильным данным.
эффективность достигается за счёт внутреннего представления вариантов в виде union с метками на уровне C.
удобство работы с такими типами трудно переоценить.

Примечание: соглашение о наименовании меток

Примеры сопоставления с образцом демонстрируют важность соглашения о наименованиях меток. По соглашению, метки начинаются с заглавной буквы, а захватываемые переменные – с малой. Без подобного соглашения возможна путаница, особенно при случайных опечатках. Например:

...
match (bop, e1, e2) {
  | (Sub, ...) => ...

  // CmpLE ошибочно набрано как CmpLe и могло бы быть воспринято как
  // захваченная переменная без указанного соглашения.
  // Но поскольку "CmpLe" начинается с заглавной буквы,
  // компилятор выдаст ошибку о неизвестной метке "CmpLe"
  | (CmpLe, ...) => ...
...
}

Рассмотрим ещё один пример, связанный с деревьями, на сей раз речь пойдёт о красно-чёрных деревьях.

[Красно-черное дерево](https://ru.wikipedia.org/wiki/%D0%9A%D1%80%D0%B0%D1%81%D0%BD%D0%BE-%D1%87%D1%91%D1%80%D0%BD%D0%BE%D0%B5%D0%B4%D0%B5%D1%80%D0%B5%D0%B2%D0%BE – это представление бинарного дерева поиска, позволяющее хранить данные, доступные по ключу за время O(log N) (при условии, что дерево хранит N элементов). Время вставки и удаления также составляет O(log N). Пример дерева, хранящего несколько целых чисел, изображён на рисунке:

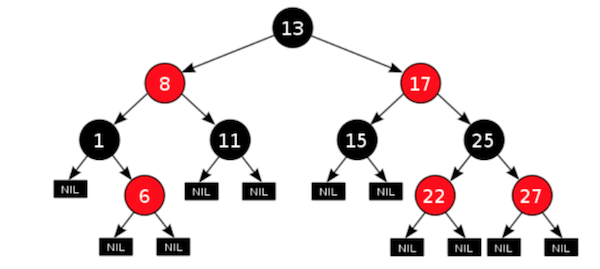
Рисунок 1. Красно-чёрное дерево

Мы можем описать подобное дерево следующим образом:

type color = Red | Black

type rbtree = Empty | RBNode: (int, color, rbtree, rbtree)

// Дерево из трёх целых чисел
val t3 = RBNode(5, Black, RBNode(1, Red, Empty, Empty),
                RBNode(10, Red, Empty, Empty))

Определение весьма напоминает абстрактное синтаксическое дерево из предыдущего примера. Реализуем простую функцию для вычисления глубины дерева:

fun depth(t: rbtree)
{
  | Empty => 0
  | RBNode(_, _, left, right) => 1+max(depth(left), depth(right))
}

Логика предельно проста и действительно похожа на псевдокод: если переданное дерево пустое, глубина равна нулю, иначе мы игнорируем цвет узла и его значение, выбираем левую и правую ветви, рекурсивно вычисляем глубину обеих подветвей и возвращаем результат 1 + max(глубина левой подветви, глубина правой подветви).

Обратите внимание, что здесь также использовалась особая форма записи функции (оператор match опущен).

Функции вставки и удаления элементов в красно-чёрное дерево здесь не показаны, они реализованы в стандартной библиотеке, см. модули Set и Map. Вместо этого перейдём к примеру реализации обобщённых структур данных.

Обобщённые варианты

Ранее мы увидели, как просто реализовать обобщённые функции обработки списков с помощью записи 't list. Что произойдёт, если захотим применить обобщённую версию типа 't rbtree? Всё окажется точно так же:

type color = Red | Black

type 't rbtree = Empty | RBNode: ('t, color, 't rbtree, 't rbtree)

// Дерево из трёх строк
val t3 = RBNode("b", Black, RBNode("a", Red, Empty, Empty),
                RBNode("c", Red, Empty, Empty))

Нам даже не понадобилось явно указывать тип для создания красно-чёрного дерева со строками.

При добавлении переменных типа конструкторы вариантов становятся обобщёнными функциями и автоматически создают экземпляр нужного типа. динственная тонкость связана с обработкой Empty – какой тип у результата? int rbtree, string rbtree или какой-то ещё? Обычно компилятор автоматически из контекста определяет нужный тип, но иногда требуется его явно указать, например:

val empty_int_rtbtree = (Empty : int rbtree)

Как изменится обработка дерева? Почти никак:

fun depth(t: 't rbtree)
{
    match t {
    | Empty => 0
    | RBNode(_, _, left, right) => 1+max(depth(left), depth(right))
    }
}

Варианты с параметрами-записями

Иногда при определении вариантов часть элементов могут содержать сложные атрибуты, тогда имеет смысл использовать в качестве атрибутов записи. Такой случай также поддерживается синтаксически.

Вот как определяется красно-чёрное дерево с использованием записей.

type color = Red | Black
type 't rbtree =
    | Empty
    | RBNode: { value: 't; clr: color;
                left: 't rbtree; right: 't rbtree }
val t3 = RBNode {
    value="b", clr=Black,
    left=RBNode { value="a", clr=Red, left=Empty, right=Empty },
    right=RBNode { value="c", clr=Red, left=Empty, right=Empty }
}

fun depth(t: 't rbtree)
{
    | Empty => 0
    // имя метки обязательно,
    // в отличие от независимо определённых записей
    | RBNode {left=l, right=r} => 1+max(depth(l), depth(r))
}

Определение записи можно прямо встраивать в определение варианта, нет необходимости определять их отдельно (хотя это может быть полезно, например, чтобы “отделить” атрибуты от метки и использовать их отдельно). Подобная нотация немного увеличивает объём текста по сравнению с кортежами, но код становится более читаемым.

Одноместные варианты

Это частный, и, на первый взгляд, бесполезный случай вариантов. Тем не менее, он может быть крайне полезным.

Предположим, мы хотим определить тип рациональных чисел и перегрузить операции для этого типа (+, -, и т.д.)

Можно определить тип следующим образоме:

type ratio_t = (int, int)
operator + ((n1, d1): ratio_t, (n2, d2): ratio_t) = ...

Мы получим конфликтом переопределения оператора + для двухместного кортежа из Builtins, так как в данном случае ratio_t не является новым типом, а является лишь псевдонимом кортежа двух целых чисел.

Проблема решается изменением определения на одноместный вариант:

type ratio_t = Ratio: (int, int)

operator + (r1: ratio_t, r2: ratio_t)
{
    val Ratio(n1, d1) = r1
    val Ratio(n2, d2) = r2
    val n = n1*d2 + n2*d1, d = d1*d2
    val k = GCD(n, d)
    Ratio(n/k, d/k)
}

// так как у нас появился отдельный тип,
// мы можем определить для него специальную функцию string()
fun string(r: ratio_t) {
    val Ratio (n, d) = r
    f"{n}/{d}"
}

// теперь код стал удобнее читать, хотя и немного увеличился в объёме
println(Ratio(1, 100) + Ratio(3, 50))

Таким образом, одноместные варианты позволяют превратить анонимные структуры в именованные, наделяя их возможностью иметь собственные наборы перегружаемых операций и функций.

Тип `option`

Мы уже встречали тип option раньше. Повторимся, что этот тип фактически не встроен в язык, а определяется в модуле Builtins следующим образом:

class 't option = None | Some: t

Кроме того, компилятор Ficus распознаёт сокращённую форму 't? наряду с традиционной формой 't option. Однако обратите внимание, что один из фундаментальных типов Ficus, на самом деле, является вариантом. Снова покажем его полезность на примере реализации функции поиска в красно-чёрном дереве.

Предположим, что узлы содержат пары (ключ, значение) и мы ищем значение, связанное с заданным ключом:

fun find_opt(t: ('key, 'value) rbtree, k0: 'key): 'value? =
match t {
| Empty => None
| RBNode((k, value), _, left, right) =>
    if k0 == k {Some(value)}
    else if k0 < k {find(left, k0)}
    else {find(right, k0)}
}

Тип option позволяет не использовать магическое значение или отдельный флаг при возврате результата из функции в случае, если значение в дереве отсутствует.

val names = [:: "Bob", "Alice", "Sam"]
for name <- names {
    match find_opt(phone_book, name) {
    | Some(number) => println(f"{name}'s phone: {number}")
    | _ => println(f"{name} is not found in the phonebook")
    }
}

Варианты

Обобщённые варианты

Варианты с параметрами-записями

Одноместные варианты

Тип option

Тип `option`